Sort and search arrays in C / C++ - PART 3

Welcome to Sort and search arrays in C / C++ - PART 3

Today I wanted to focus my attention on the searching algorithm. Let's find some integers!

First I will start with the most simple implementation which brute-force iterates through each integer until it finds what it wants.

The code to do this is super simple....

//
// the most basic brute-force index of
//
int array_indexof(int a[], int len, int value) {
    // loop through our items in reverse
    for (int i = len-1; i >= 0; i--) {
        // if we find the value, return the index
        if (a[i] == value) return i;
    }

    // if we get here, we didn't find it, return -1
    return -1;
}

Even though this is not efficient, it is still ridiculously fast, this is because generally the slowest operations are data manipulation. Newer CPU's are fantastic at prefetching steams of data by using branch prediction. If you are not familiar with branch prediction, I really suggest you go search and have a read about how it works.

Regardless, we want to optimise our function, so we will again be using divide and conquer.

First I wanted to give an example of partitioning, this method would be faster than our original but it is completely pointless.

//
// a useless version of our function that partitions the array and searches 1 or the other half
//
int array_indexof2(int a[], int len, int value) {
    int pivot = len/2;

    if ((len > 1) && (a[pivot] > value)) {
        // search the first half of the array
        for (int i = 0; i < pivot; i++) {
            // if we find the value, return the index
            if (a[i] == value) return i;
        }

    } else {
        // search the second half of the array in reverse
        for (int i = pivot; i >= 0; i--) {
            // if we find the value, return the index
            if (a[i] == value) return i;
        }
    }

    // if we get here, we didn't find it, return -1
    return -1;
}

I just wanted to show what is the point of partitioning. Here we can see depending on the middle value of our array, we will search either the lower or the upper half of the array. So with divide and conquer what we want to achieve is to keep dividing the array by the divided (or middle) index.

Writing such a function is actually even more simple than this indexof2 function.

//
// divide and conquer style indexof, also known as binary search
//
int array_dacindexof(int a[], int len, int value) {
    // partition lower index, which starts at the array zero position
    int lower = 0;
    // partition upper index, this is the length of the array -1 (because 0-index)
    int upper = len-1;

    // while the lower index is lower or equal to the upper we keep partitioning and searching
    while (lower <= upper) {
        // we set the current index as the lower + upper and divide it by 2. This gives us a position between the 2 positions.
        int index = (lower + upper) / 2;

        // if by luck the item at index is the value we want, just return
        if (a[index] == value) return index;
        // else if the item at index is lower than our value we will move our partition lower index up to this point + 1
        else if (a[index] < value) lower = index + 1;
        // else we move our partition upper index to our current index - 1 and the while will continue
        else upper = index - 1;
    }
    
    // if we finished the while loop without a result, it doesn't exist, return -1
    return -1;
}

I have commented the code step by step. This is one of the most easiest indexof functions to write.

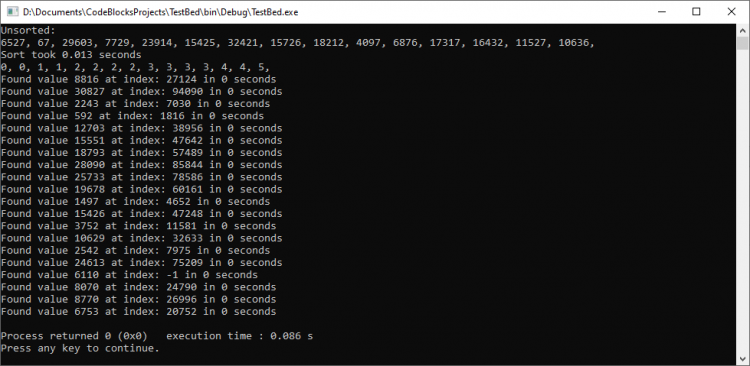
I have updated the original code main function to run the dac index of 20 times.

int main() {
    // a constant number we can change easily, how large the array will be.
    const int ARRAY_SIZE = 100000;

    // declare our array
    int a[ARRAY_SIZE];

    // call our fill function
    array_fillrand(a, ARRAY_SIZE);
    //int a[] = {5, 1, 15, 9872, 42, 2576, 234, 4, 557, 4, 78, 353464, 32534, 47523, 2};

    // this is useless as we know the size already, but I want to keep it as in another
    // article we may go into sorting dynamic sized arrays
    int len = sizeof(a) / sizeof(int);

    // printing this amount of numbers is crazy, we will modify our print function to print
    // only the first 15 numbers so we can see a snapshot of it working...
    std::cout << "Unsorted: " << std::endl;
    array_print(a, len);

	// get start tick
	int start_tick = clock();

	// sort the array
	// array_heapsort(a, len);
	array_dacsort(a, 0, len-1);

	// get end tick
	int end_tick = clock();

	// output the difference to get total tick count, but we will convert to seconds
	std::cout << "Sort took " << ((float)end_tick - start_tick) / CLOCKS_PER_SEC << " seconds" << std::endl;

	// print sorted array
	array_print(a, len);

	srand(rand());

	for (int c = 0; c < 20; c++) {
        int getindex = rand();
        // let's find our number
        start_tick = clock();
        int index = array_dacindexof(a, len, getindex);
        end_tick = clock();

        std::cout << "Found value " << getindex << " at index: " << index << " in " << ((float)end_tick - start_tick) / CLOCKS_PER_SEC << " seconds" << std::endl;
	}
    return 0;
}

After I finished writing this dac index function, I done some searching to see if anyone had divised a better way of doing it, but it seems this is considered the best way of doing it.

I wanted to just add that an unsorted array, you could only use the linear indexof, however, we could slightly improve this function by removing the count index comparison.

When declaring our array, we add an additional array entry at the end (This could be modified to work with multi threaded read access to the array)

So we update our main to be like so:

// a constant number we can change easily, how large the array will be.
    const int ARRAY_SIZE = 500000;

    // declare our array
    int a[ARRAY_SIZE+1]; // we are going to add 1 extra as our failsafe for unsorted find

    // call our fill function
    array_fillrand(a, ARRAY_SIZE);

Notice our declaration has +1 for an additional array that won't be filled or used in general, except for our linear index of.

//
// a linear index of that has a failsafe value so we don't need to compare the current index
//
int array_indexof_fs(int a[], int len, int value) {
    // this is our failsafe, we add the value in our empty array item so it is 100% sure the while will find the value
    // even if it does not exist in our array
    a[len] = value;

    // starting from the 0-index
    int i = 0;

    // now we can just do a single compare until we find the value, if it doesn't exist we will hit our failsafe
    while (a[i++] != value);

    // if the index is the length of the array we didn't find it else return the actual index
    return (i == len) ? -1 : i;
}

So this version of the indexof will save 1 compare instruction per array item at the cost of 1 mov and a cmp at the end.

And on that note, I will wrap this post up with the full code we have so far.

/*
    ! *****************************************************************************

    MIT License

    Copyright (c) Colin J.D. Stewart. All rights reserved.

    The following license applies to this software and associated documentation 
    files (the "Software"):

    Permission is hereby granted, free of charge, to any person obtaining a copy 
    of this Software, to use, copy, modify, merge, publish, distribute, sublicense, 
    and/or sell copies of the Software, subject to the following conditions:

    1. 	The above copyright notice and this permission notice shall be included 
        in all copies or substantial portions of the Software.
        
    2. 	If you use this Software in a product or service, an attribution in the 
        form of a copyright notice, a link to the license, and a disclaimer of 
        warranties (and any other similar attribution) is required for any 
        distribution, reproduction, or derivative works of the Software.

    THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR 
    IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
    FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL 
    THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES, OR 
    OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT, OR OTHERWISE, 
    ARISING FROM, OUT OF, OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR 
    OTHER DEALINGS IN THE SOFTWARE.

    ! ***************************************************************************** 
*/

#include <iostream>
#include <time.h>



//
// divide and conquer quicksort implementation.
//
void array_dacsort(int a[], int lower, int upper) {
    // if lower index is higher or equal to upper just return
    if (lower >= upper) return;

    // let's start to calculate the pivot of the partition starting with the passed upper index of the array
    int pivot = a[upper];
    // we will use "i" as a track index
    int i = lower - 1;

    // loop through our array from lower to upper indexes
    for (int j = lower; j < upper; j++)
        // if the value of the current index is lower than the array pivot, we should increment the track index and swap the values
        if (a[j] < pivot) std::swap(a[++i], a[j]);

    // swap the last upper value with the current track index + 1
    std::swap(a[i+1], a[upper]);

    // now we will do a recursive call to sort the 2 partitioned parts
    array_dacsort(a, lower, i);
    array_dacsort(a, i+2, upper);
}


//
// procedure to re-arrange values obeying heap properties.
//
inline void array_heapify(int a[], int parent, int len) {
    // upper is our current upper maximum index
    int upper = parent;

    // simple while loop
    while (true) {
        // set the left index like a binary tree, we want the left child which is parent * 2 + 1
        // use bitwise instead of multiplication
        int left = (parent << 1) + 1;
        // right is 1 index higher
        int right = left + 1;

        // self explanatory
        if ((left < len) && (a[left] > a[upper])) upper = left;
        if ((right < len) && (a[right] > a[upper])) upper = right;
        if (upper == parent) break;

        std::swap(a[parent], a[upper]);

        parent = upper;
    }
}


//
// our heapsort procedure that is basically the loops calling our re-arrange
//
void array_heapsort(int a[], int len) {
    // make sure we have at least 2 items
    if (len < 2) return;

    // build the heap
    for (int i = (len / 2 - 1); i >= 0; i--)
        array_heapify(a, i, len);

    // sort the heap
    for (int i = len - 1; i >= 0; i--) {
		// swap the root element
        std::swap(a[0], a[i]);
		// re-arrange using our heapify procedure
        array_heapify(a, 0, i);
    }
}

//
// procedure to sort the array
//
void array_sort(int a[], int len) {
    // make sure we have at least 2 items
    if (len < 2) return;

    // let's run through the input array starting from the second item
    for (int i = 1; i < len; i++) {
        // store the value of index "i" for later and so we don't need to keep accessing the array offset
        int value = a[i];
        // j set as the current index and used to go in reverse through the array
        int j = i;

        // while the current index is above the first item and
        // the value of the item before the current index is above our value THEN
        while ((j > 0) && (a[j-1] > value)) {
            // set the value at current index to the previous value
            a[j] = a[j-1];
            // decrement our j index to continue our while condition
            j--;
        }

        // finally set the value of whatever our current index is to the saved value earlier
        a[j] = value;
    }
}



//
// the most basic loop to find the index of a value
//
int array_indexof(int a[], int len, int value) {
    // loop through our items in reverse
    for (int i = len-1; i >= 0; i--) {
        // if we find the value, return the index
        if (a[i] == value) return i;
    }

    // if we get here, we didn't find it, return -1
    return -1;
}


//
// a linear index of that has a failsafe value so we don't need to compare the current index
//
int array_indexof_fs(int a[], int len, int value) {
    // this is our failsafe, we add the value in our empty array item so it is 100% sure the while will find the value
    // even if it does not exist in our array
    a[len] = value;

    // starting from the 0-index
    int i = 0;

    // now we can just do a single compare until we find the value, if it doesn't exist we will hit our failsafe
    while (a[i++] != value);

    // if the index is the length of the array we didn't find it else return the actual index
    return (i == len) ? -1 : i;
}

//
// divide and conquer style indexof, also known as binary search
//
int array_dacindexof(int a[], int len, int value) {
    // partition lower index, which starts at the array zero position
    int lower = 0;
    // partition upper index, this is the length of the array -1 (because 0-index)
    int upper = len-1;

    // while the lower index is lower or equal to the upper we keep partitioning and searching
    while (lower <= upper) {
        // we set the current index as the lower + upper and divide it by 2. This gives us a position between the 2 positions.
        int index = (lower + upper) / 2;

        // if by luck the item at index is the value we want, just return
        if (a[index] == value) return index;
        // else if the item at index is lower than our value we will move our partition lower index up to this point + 1
        else if (a[index] < value) lower = index + 1;
        // else we move our partition upper index to our current index - 1 and the while will continue
        else upper = index - 1;
    }

    // if we finished the while loop without a result, it doesn't exist, return -1
    return -1;
}


//
// print array values
//
void array_print(int a[], int len) {
    // we have modified this to show a max of 15 items
    for (int i = 0; i < ((len > 15) ? 15 : len); i++) {
        std::cout << a[i] << ", ";
    }
    std::cout << std::endl;
}



//
// fill an array with random integers
//
void array_fillrand(int a[], int len) {
    // Set random seed based on current time
    srand(1987);

    // generate random numbers
    for (int i = 0; i < len; i++) {
        a[i] = rand();
    }
}


//
// our starting point
//
int main() {
    // a constant number we can change easily, how large the array will be.
    const int ARRAY_SIZE = 100000;

    // declare our array
    int a[ARRAY_SIZE];

    // call our fill function
    array_fillrand(a, ARRAY_SIZE);
    //int a[] = {5, 1, 15, 9872, 42, 2576, 234, 4, 557, 4, 78, 353464, 32534, 47523, 2};

    // this is useless as we know the size already, but I want to keep it as in another
    // article we may go into sorting dynamic sized arrays
    int len = sizeof(a) / sizeof(int);

    // printing this amount of numbers is crazy, we will modify our print function to print
    // only the first 15 numbers so we can see a snapshot of it working...
    std::cout << "Unsorted: " << std::endl;
    array_print(a, len);

	// get start tick
	int start_tick = clock();

	// sort the array
	// array_heapsort(a, len);
	array_dacsort(a, 0, len-1);

	// get end tick
	int end_tick = clock();

	// output the difference to get total tick count, but we will convert to seconds
	std::cout << "Sort took " << ((float)end_tick - start_tick) / CLOCKS_PER_SEC << " seconds" << std::endl;

	// print sorted array
	array_print(a, len);

	srand(rand());

	for (int c = 0; c < 20; c++) {
        int getindex = rand();
        // let's find our number
        start_tick = clock();
        int index = array_dacindexof(a, len, getindex);
        end_tick = clock();

        std::cout << "Found value " << getindex << " at index: " << index << " in " << ((float)end_tick - start_tick) / CLOCKS_PER_SEC << " seconds" << std::endl;
	}
    return 0;
}

As I noted in the previous article on this subject, I will probably convert this into a c++ library for re-usability and will add sorting of different types of data.

Until next time.....